| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 스토리북
- 알고리즘
- 우선순위 큐
- 블록체인
- 풀이
- React
- algorithm
- C++
- baekjoon
- 기본 수학 2단계
- frontend
- Console
- bip39
- 에러
- Blockchain
- SASS
- 기본수학1단계
- 니모닉
- priority queue
- 프로그래밍
- 리액트
- SVG
- TypeScript
- three.js
- Mnemonic
- 백준
- 지갑
- 코딩
- Storybook
- scss
- Today
- Total
Moong
[백준 11729번][C++] 백준 하노이 탑 이동 순서 본문
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
출력
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
풀이
Algorithm
- 문제 이해하기

하노이 탑의 원리를 애니메이션으로 나타낸 것을 보면, 4개의 원판을 옮길 때, 1~3번 원판이 모두 중간으로 옮겨진 후에야 가장 큰 4번째 원판을 세 번째 장대로 옮길 수 있다. 이 과정 후에 다시 중간에 있던 1~3번 원판들을 세 번째 장대로 옮김으로써 마지막 장대로 모두 이동시킨다.
이처럼 큰 틀로 하노이 원판의 알고리즘을 바라보면,
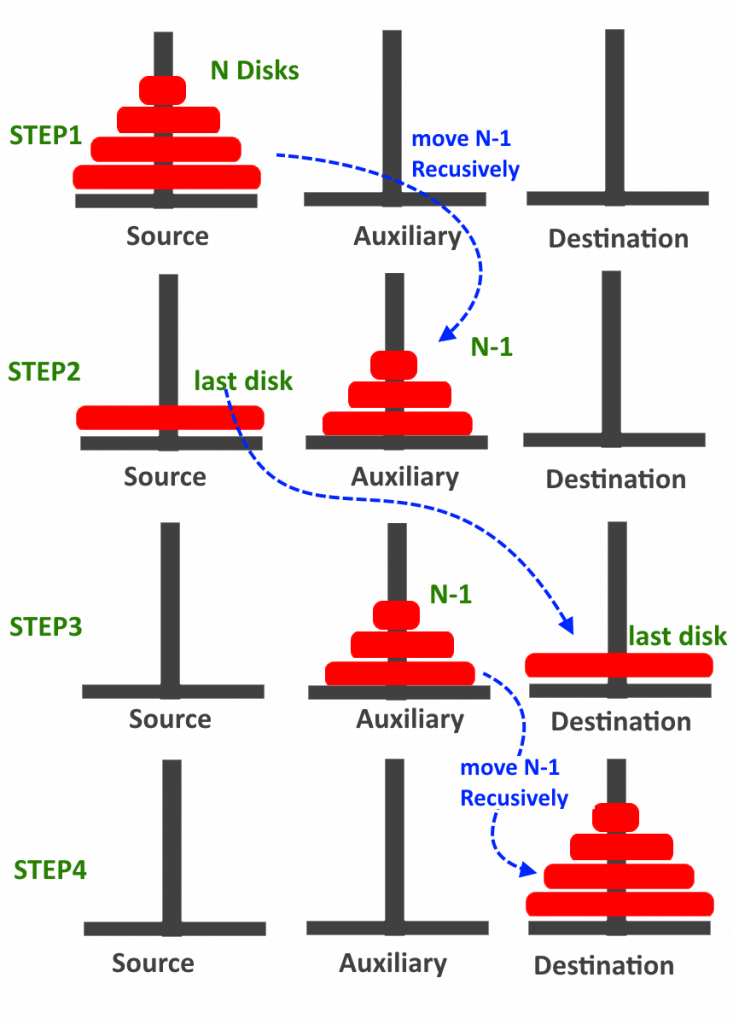
1~N-1의 원판을 중간 자리로 옮김 → N번째 원판을 목표한 장대로 옮김 → 1~N-1의 원판을 목표한 장대로 옮김
의 순서로 나타날 것이다. 이 시각으로 문제에 접근해보자.
- 옮긴 횟수를 리턴하는 함수 Hanoi_num
int Hanoi_num(int N) {
if (N == 1)
return 1;
return Hanoi_num(N - 1) * 2 + 1;
}- 1~N-1까지의 원판을 중간 자리로 옮길 때 : Hanoi_num(N-1)번
- N번째 원판을 목표한 장대로 옮길 때 : 1번
- 1~N-1까지의 원판을 목표한 장대로 옮길 때 : Hanoi_num(N-1)번
그래서 모두 합하면 Hanoi_num(N-1)*2+1번이다.
- Base case : N이 1이라면, 이동 sequence가 1 3으로 한번밖에 되지 않는다.
- 옮기는 과정을 출력하는 함수 Hanoi_seq
void Hanoi_seq(int N, int start, int end, int nothing) {
if (N == 1)
cout << start << ' ' << end << '\n';
else {
Hanoi_seq(N - 1, start, nothing, end); // 1부터 N-1까지의 탑을 start에서 nothing으로 보낸다.
cout << start << ' ' << end << '\n'; // N번째 원판을 start에서부터 end로 보낸다.
Hanoi_seq(N - 1, nothing, end, start); // 1부터 N-1까지의 탑을 nothing에서 end로 보낸다.
}
}여기에서 자신이 존재하는 장대의 번호를 start, 자신이 이동해야 하는 장대를 end, 그 어떤 것도 아닌 장대를 nothing이라고 합시다.
그렇다면
- 1~N-1까지의 원판을 아무것도 아닌 자리로 옮길 때 Hanoi_seq(N-1, start, nothing, end);
- N번째 원판을 목표한 장대로 옮길 때 cout << start << ' ' << end << '\n';
- 1~N-1까지의 원판을 다시 목표한 장대로 옮길 때 Hanoi_seq(N-1, nothing, end, start);의 코드로 나타낼 수 있습니다.
- Base case : N이 1이라면 처음 있던 곳에서 목표하는 지점으로 가기만 하면 되기 때문에 그냥 cout << start << ' ' << end << '\n';입니다.
code
#include <iostream>
using namespace std;
int Hanoi_num(int N) {
if (N == 1)
return 1;
return Hanoi_num(N - 1) * 2 + 1;
}
void Hanoi_seq(int N, int start, int end, int nothing) {
if (N == 1)
cout << start << ' ' << end << '\n';
else {
Hanoi_seq(N - 1, start, nothing, end); // 1부터 N-1까지의 탑을 start에서 nothing으로 보낸다.
cout << start << ' ' << end << '\n'; // N번째 원판을 start에서부터 end로 보낸다.
Hanoi_seq(N - 1, nothing, end, start); // 1부터 N-1까지의 탑을 nothing에서 end로 보낸다.
}
}
int main() {
int N;
cin >> N;
cout << Hanoi_num(N) << '\n';
Hanoi_seq(N, 1, 3, 2);
return 0;
}'Baekjoon' 카테고리의 다른 글
| [백준 15649번][C++] N과 M (1) (0) | 2021.08.09 |
|---|---|
| [Baekjoon-2231번][C++] 백준 분해합 (0) | 2021.01.20 |
| [백준 1002번][C++] 백준 터렛 (0) | 2021.01.18 |
| [백준 4948번][C++] 백준 베르트랑 공준 (0) | 2021.01.14 |
| [백준 11653번][C++] 백준 소인수분해 (0) | 2021.01.14 |

